Calicut University M Tech Structural Engineering Syllabus

Provide me the syllabus of Calicut University’s M.Tech Structural Engineering which is a branch of Civil engineering along with the schema of the exam of M.Tech Structural Engineering from Calicut University?

Can you provide me the syllabus of M. Tech Structural Engineering (Civil Engineering) Program offered by University of Calicut as I need it for preparation of the exam?

[pooja]

The syllabus of M. Tech Structural Engineering (Civil Engineering) Program offered by University of Calicut is as follows:

SEMESTER 1
CES10 101 NUMERICAL METHODS IN STRUCTURAL ENGINEERING

Module I (14 Hours)
Systems of linear algebraic equations:
Elimination and factorization methods: Gauss, Cholesky and Crouts methods Ill-conditioned systems Symmetric and Banded systems Gauss Siedel iteration - Relaxation method-condition of convergence of iterative methods. Systems of non-linear equations Newton-Raphson Method

Module II (16 Hours)
Partial differential equations:
Ordinary differential equations in more than two variables first order P.D.E-integral surface passing through a given curve-surfaces orthogonal to given system-compatible systems of first order P.D. Echarpits method -solution satisfying the given conditions-linear P .D.E with constant coefficients

Module III (12 Hours)
Interpolation and integration
Lagrange Hermitian and cubic spline methods Isoparametric style of interpolation Numerical Integration using Gaussian quadrature - One and Two Dimensions Gauss Hermite Quadrature Method - NewtonCotes open quadrature - Monte Carlo Method - Application to deflection of beams and plates

Module IV (12 Hours)
Eigen Value Problems
Introduction Methods of solutions: method of characteristic polynomial Faddeev-Leverrier Method - Approximate Methods:- Forward iteration, inverse iteration (Vianello-Stoodala method) Power Method with deflation - Rayleigh Ritz Method.

Text Books:
1. B.S Grewal, Numerical Methods in Engineering and Science, Khanna Publications
2. Rajasekaran S, Numerical Methods in Science and Engineering A practical approach, AH Wheeler & Co.
3. P Kandasamy, Numerical Methods, S Chand and company.
4. Stevan C. Chapra and Raymond P. Canale, Numerical Methods for Engineers, McGraw Hill
5. Erwin Kreyszig ., Advanced Engineering Mathematics, 5th Edition, Weiley Eastern Ltd., 1989.

References:
6. Michael D Greenberg, Advanced Engineering Mathematics, Pearson education.
7. Ian Sneddon, Elements of Partial Differential Equations, McGraw Hill, International Editions
8. Balagurusamy , Numerical Methods, Tata McGraw Hill
9. Carrier, G.F. and Pearson, C.E., Partial Differential Equations, Academic Press, New York, 1976
10. Carl de Boor Verlog, A practical guide to splines, Springer-Verlag


Syllabus M. Tech Structural Engineering (Civil Engineering) University of Calicut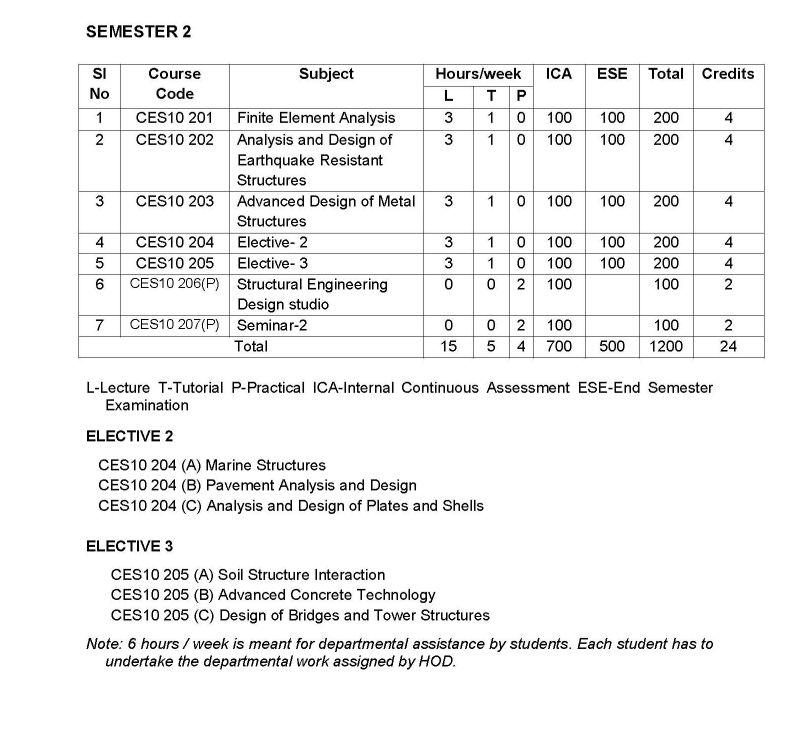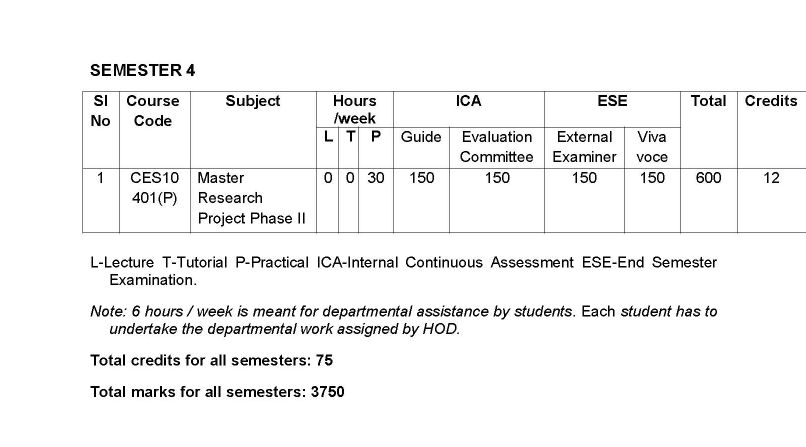